Как найти площадь треугольника

Формулы площади треугольника

1. Формула площади треугольника по стороне и высотеПлощадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

   S =	1
   2

2. Формула площади треугольника по трем сторонам

   S = √()()()

3. Формула площади треугольника по двум сторонам и углу между ними
   Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

   S =	1
   2

4. Формула площади треугольника по трем сторонам и радиусу описанной окружности

   S =
   4R

5. Формула площади треугольника по трем сторонам и радиусу вписанной окружностиПлощадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

   S =  ·

   где S — площадь треугольника, — длины сторон треугольника, — высота треугольника, — угол между сторонами и , — радиус вписанной окружности,
   R — радиус описанной окружности,

   =	+  +	— полупериметр треугольника.
   2

Калькулятор площади треугольника по трем сторонам

Как известно, треугольником принято называть плоскую геометрическую фигуру, многоугольник, который ограничен минимальным количеством сторон. Также, стоит помнить, что всякий многоугольник делится на определённое количество треугольников.

Для этого необходимо соединить его вершины такими отрезками, которые не пересекали бы его стороны. Вот почему, зная как рассчитать площадь треугольника, Вы можете получить площадь большинства геометрических фигур.

Формула Герона для вычисления площади треугольника по трем сторонам

В том случае если нам известны параметры каждой стороны нашего треугольника, мы можем рассчитать площадь фигуры по формуле Герона. Для её упрощения следует применить новую величину, так называемый полупериметр, который является суммой всех сторон треугольника, которая разделена пополам.

После получения значения полупериметра, Вы можете приступать к расчёту площади по руководствуясь следующей формулой: S = sqrt(p(p-a)(p-b)(p-c)), в которой «p» – полупериметр, «a,b,c» – стороны фигуры и sqrt –квадратный корень.

Пример вычисления площади треугольника по трем сторонам

Рассмотрим на примере вычисление площади треугольника по формуле Герона.

p = (a + b + c)/ 2  где p – половина периметра треугольника.

таким образом S = √ p ( p – a ) ( p – b ) ( p – c ) .

(Это также называется формулой Герона)

Дано:

Треугольник со сторонами a = 4, b = 5, c = 3.

Задание:Найдите площадь треугольника

Решение:

Используйте формулу половинного периметра:

p = (3 + 4 + 5)/ 2= 6

Полученные значения подставляем в формулу Герони:

S = √ 6 ( 6 – 3 ) ( 6 – 4 ) ( 6 – 5 ) =

√ 6 ⋅ 3 ⋅ 2 ⋅ 1 = √ 36 =6

Ответ: 6

Историческая справка

Формула приписывается Герону, живущему в  Александрии, который был греческим инженером и математиком в 10 – 70 годах нашей эры

Среди прочего, он разработал  первый известный паровой двигатель, но его рассматривали как игрушку!

Понятие площади

Понятие площади любой геометрической фигуры, в частности треугольника, будем связывать с такой фигурой, как квадрат. За единицу площади любой геометрической фигуры будем принимать площадь квадрата, сторона которого равняется единице. Для полноты, вспомним два основных свойства для понятия площадей геометрических фигур.

Свойство 1: Если геометрические фигуры равны, то значения их площадей также равны.

Свойство 2: Любая фигура может быть разбита на несколько фигур. Причем площадь первоначальной фигуры равняется сумме значений площадей всех составляющих её фигур.

Рассмотрим пример.

Пример 1

Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице

Решение.

Очевидно, что одна из сторон треугольника является диагональю прямоугольника, у которого одна сторона имеет длину $5$ (так как $5$ клеток), а вторая $6$ (так как $6$ клеток). Следовательно, площадь этого треугольника будет равняться половине такого прямоугольника. Площадь прямоугольника равняется

$5\cdot 6=30$

Тогда площадь треугольника равняется

$30:2=15$

Ответ: $15$.

Далее рассмотрим несколько методов для нахождения площадей треугольников, а именно с помощью высоты и основания, с помощью формулы Герона и площадь равностороннего треугольника.

Примеры решения задач

Разберемся с нахождением площади треугольника наглядно на примере некоторых случаев.

Задача 1

В треугольник вписана окружность с радиусом 6 см. Известно, что его стороны равны 10 см, 12 см и 14 см. Определить площадь фигуры.

Решение

Для расчета будем использовать формулу \(S=r\times\frac{a+b+c}2\) или \(S=r\times p\). Подставляем имеющиеся значения и получается:

\(S=6\times\frac{10+12+14}2=6\times18=108\) \(см^2\)

Ответ: \(108\) \(см^2\).

Задача 2

Дан равносторонний треугольник, вокруг которого описали окружность с радиусом 3 см. Посчитать S данной фигуры.

Решение

Считать будем, опираясь на следующее уравнение \(S=\frac{3\sqrt3R^2}4\). Подставляем данные величины и получаем:

\(S=\frac{3\sqrt33^2}4=\frac{27\sqrt3}4 см^2\)

Ответ: \(\frac{27\sqrt3}4 см^2.\)

Задача 3

Известно, что у равнобедренного треугольника основание равно 4 см, а стороны по 3 см. Нужно вычислить площадь фигуры.

Решение

Для расчета S используем формулу \(S=\frac b4\sqrt{4a^2-b^2}\). Получается:

\(\frac44\sqrt{4\times3^2-4^2}=\sqrt{36-16}=\sqrt{20}=2\sqrt5 см^2\)

Ответ: \(2\sqrt5 см^2.\)

Задача 4

Дан треугольник с прямым углом, у которого гипотенузы равна 2 см, а один из острых углов равен \(30^\circ\). Узнать S данной фигуры.

Решение

Для расчетов будем ориентировать на следующее уравнение: \(S=c^2\times\cos\left(\alpha\right)\times\sin\left(\alpha\right)\). Подставляем известные значения:

\(S=2^2\times\frac{\sqrt3}2\times\frac12=\sqrt3 см^2\)

Площадь треугольника формула

*То есть если нам будет известна любая сторона треугольника и высота опущенная на эту сторону, то мы всегда сможем вычислить площадь этого треугольника.

Формула вторая

Как уже было изложено в статье о площади параллелограмма формула имеет вид:

Площадь треугольника равна половине его площади, значит:

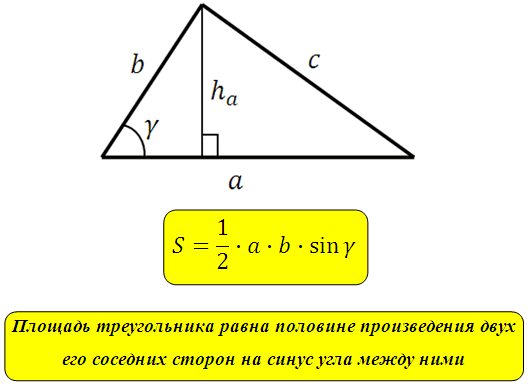
*То есть если будут известны любые две стороны в треугольнике и угол между ними, мы всегда сможем вычислить площадь такого треугольника.

Формула Герона (третья)

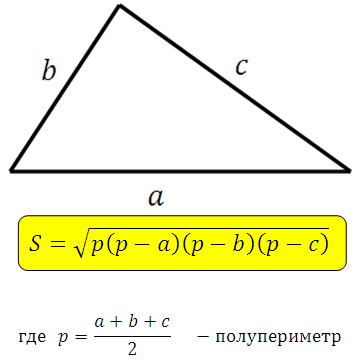
Данную формулу выводить сложно и вам это ни к чему. Посмотрите какая она красивая, можно сказать, что сама запоминается.

*Если даны три стороны треугольника, то по данной формуле мы всегда можем вычислить его площадь.

Формула четвёртая

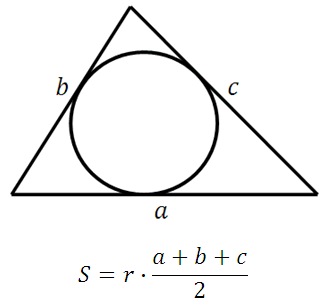
где r – радиус вписанной окружности

*Если известны три стороны треугольника и радиус вписанной в него окружности, то мы всегда можем найти площадь этого треугольника.

Формула пятая

где R – радиус описанной окружности.

*Если известны три стороны треугольника и радиус описанной около него окружности, то мы всегда можем найти площадь такого треугольника.

Возникает вопрос: если  известны три стороны треугольника, то не проще ли его площадь найти по формуле Герона!

Да, бывает проще, но не всегда, иногда возникает сложность. Это связано с извлечением корня. Кроме того, данные формулы очень удобно применять в задачах, где дана площадь треугольника, его стороны и требуется найти радиус вписанной или описанной окружности. Такие задания имеются  в составе ЕГЭ.

Давайте отдельно рассмотрим формулу:

Она является частным случаем формулы площади многоугольника, в который вписана окружность:

Рассмотрим её на примере пятиугольника:

Соединим центр окружности с вершинами данного пятиугольника и опустим из центра перпендикуляры к его сторонам. Получим пять треугольников, при чём  опущенные перпендикуляры являются радиусами вписанной окружности:

Площадь пятиугольника равна:

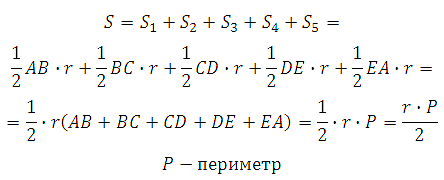
Теперь понятно, что если речь идёт о треугольнике, то данная формула приобретает вид:

Формула шестая

Пусть сторона треугольника равна a, из противоположной вершины к этой стороне проведён произвольный отрезок образующий с ней угол (фи):

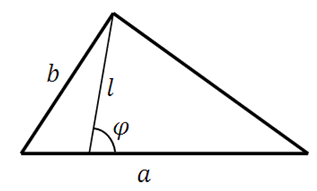
Тогда

Данная формула используется очень редко на практике, возможно вы её видите впервые, ну так просто написал, чтобы знали. Её ещё можно вывести преобразовав формулу площади четырёхугольника:

Также она является следствием из :

Что добавить? Есть ещё формулы треугольника связанные с координатами  вершин, векторами на которых он построен. Об этом будет статья в будущем, не пропустите!

Площадь прямоугольного треугольника. Тут всё просто — она равна половине площади прямоугольника, то есть одной второй произведения катетов.

На этом всё! Успеха Вам!

Как найти площадь треугольника через высоту и основание

Теорема 1

Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.

Математически это выглядит следующим образом

$S=\frac{1}{2}αh$

где $a$ — длина стороны, $h$ — высота, проведенная к ней.

Доказательство.

Рассмотрим треугольник $ABC$, в котором $AC=α$. К этой стороне проведена высота $BH$, которая равняется $h$. Достроим его до квадрата $AXYC$ как на рисунке 2.

Площадь прямоугольника $AXBH$ равняется $h\cdot AH$, а прямоугольника $HBYC$ равняется $h\cdot HC$. Тогда

$S_ABH=\frac{1}{2}h\cdot AH$, $S_CBH=\frac{1}{2}h\cdot HC$

Следовательно, искомая площадь треугольника, по свойству 2, равняется

$S=S_ABH+S_CBH=\frac{1}{2}h\cdot AH+\frac{1}{2}h\cdot HC=\frac{1}{2}h\cdot (AH+HC)=\frac{1}{2}αh$

Теорема доказана.

Пример 2

Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице

Решение.

Основание этого треугольника равняется $9$ (так как $9$ составляет $9$ клеток). Высота также равняется $9$. Тогда, по теореме 1, получим

$S=\frac{1}{2}\cdot 9\cdot 9=40,5$

Ответ: $40,5$.

Провести расчеты сможет помочь геометрия

Расчет площади фронтона способом параллелограмма: чтоб определить площадь треугольника-фронтона, нужно увеличить мнимой линией треугольник до параллелограмма и сосчитать его площадь по формуле S=ah, где, S – площадь всего параллелограмма, a – длина основания, h – высота параллелограмма и фронтона. Полученное значение нужно поделить на 2 — это и есть площадь треугольного фронтона.

Провести нужный расчет, чтоб узнать площадь системы, смогут помочь знания геометрии и калькулятор. При треугольной форме, конек будет выступать вершиной треугольника. Его высота — это катет прямоугольного треугольника. Роль второго катета выполняет ширина дома при односкатной крыше. При двускатной — это ширина дома, поделённая на 2. И при шатровой — диагональ дома, поделённая на 2. Расчет высоты конька можно сделать, умножив длину катета на тангенс угла уклона конструкции кровли. Таблицу тангенсов есть прекрасная возможность найти в учебнике по геометрии.

К примеру, у дома, ширина какого 10 м строится двускатная крыша, уклон какой 35 градусов. Тангенс 35 градусов — 0,7. Подобным образом, высота фронтона: 10/2х0,7=3,5 м. Зная это значение можно определить площадь треугольника. Тут снова сможет помочь калькулятор: высота умножается на длину основания и результат который получился разделяется на два. В приведенном примере это значение будет: 3,5х10/2=17,5 метров квадратных.

Расчет площади фронтона способом треугольника: вычислить можно ее, зная углы наклона фронтона и геометрические формулы вычисления площади треугольников.

Площадь трапециевидного фронтона также очень легко высчитать. Необходимо сложить длину оснований трапеции и поделить это значение пополам, а потом помножить на высоту. К примеру, если трапеция имеет высоту 2 м и основания вверху 4 м и внизу 10 м, то ее площадь будет равняется 4+10/2*2=14 метров квадратных.

Если крыша с более сложной конфигурацией и несколькими фронтонами, к примеру, с четырьмя, то для удобства ее нужно разбить на простые геометрические составляющие. В данном случае, расчет проходит для всех 4 фронтонов кровли, другими словами для любой геометрической фигуры. Для наглядности можно составить чертежи. Подобным вариантом поступить и с кровлей на 3 фронтона.

Часто изготавливается слуховое окно. Назначение окна бывает очень разным, как декоративным, так и практичным. По любому площадь его вычитается из общего значения.

При расчитывании на срубе, ширина стен указывается по осям бревен, другими словами по самому центру, не беря во внимание выпуски на перерубы. https://www.youtube.com/embed/fOlIW8FXVP8

https://youtube.com/watch?v=fOlIW8FXVP8

Медианы треугольника

Определение. Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника:

1. Медианы треугольника пересекаются в одной точке. (Точка пересечения медиан называется центроидом)

2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

   AOOD = BOOE = COOF = 21

3. Медиана треугольника делит треугольник на две равновеликие части

   S_∆ABD = S_∆ACD

   S_∆BEA = S_∆BEC

   S_∆CBF = S_∆CAF

4. Треугольник делится тремя медианами на шесть равновеликих треугольников.

   S_∆AOF = S_∆AOE = S_∆BOF = S_∆BOD = S_∆COD = S_∆COE

5. Из векторов, образующих медианы, можно составить треугольник.

Формула Герона

Теорема 2

Если нам даны три стороны треугольника $α$, $β$ и $γ$, то его площадь можно найти следующим образом

$S=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$

здесь $ρ$ означает полупериметр этого треугольника.

Доказательство.

Рассмотрим следующий рисунок:

По теореме Пифагора из треугольника $ABH$ получим

$h^2=γ^2-x^2$

Из треугольника $CBH$, по теореме Пифагора, имеем

$h^2=α^2-(β-x)^2$

$h^2=α^2-β^2+2βx-x^2$

Из этих двух соотношений получаем равенство

$γ^2-x^2=α^2-β^2+2βx-x^2$

То есть

$x=\frac{γ^2-α^2+β^2}{2β}$

Получим

$h^2=γ^2-(\frac{γ^2-α^2+β^2}{2β})^2$

$h^2=\frac{(α^2-(γ-β)^2 )((γ+β)^2-α^2)}{4β^2}$

$h^2=\frac{(α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α)}{4β^2}$

Так как $ρ=\frac{α+β+γ}{2}$, то $α+β+γ=2ρ$, значит

$h^2=\frac{2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α)}{4β^2}$

$h^2=\frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2 }$

$h=\sqrt{\frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2}}$

$h=\frac{2}{β}\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$

По теореме 1, получим

$S=\frac{1}{2} βh=\frac{β}{2}\cdot \frac{2}{β} \sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$

Теорема доказана.

Формулы площади треугольника

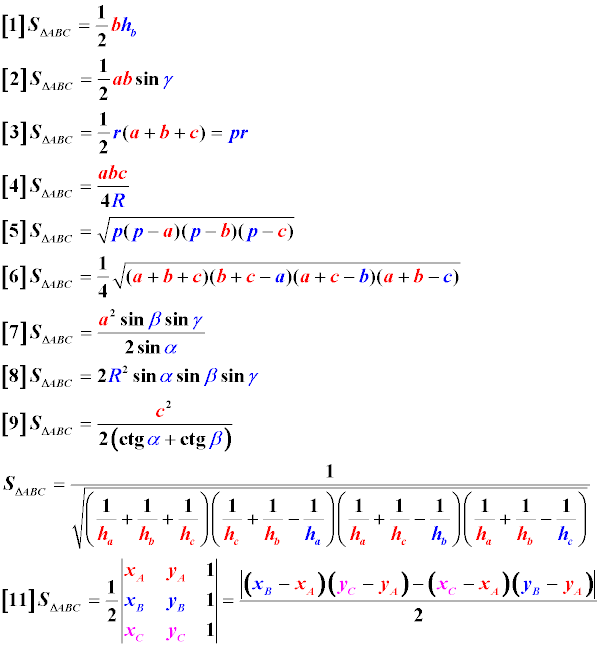
Пояснения к формулам: a, b, c — длины сторон треугольника, площадь которого мы хотим найти r — радиус вписанной в треугольник окружности R — радиус описанной вокруг треугольника окружности h — высота треугольника, опущенная на сторону p — полупериметр треугольника, 1/2 суммы его сторон (периметра) α — угол, противолежащий стороне a треугольника β — угол, противолежащий стороне b треугольника γ — угол, противолежащий стороне c треугольника h_a, h_b, h_c — высота треугольника, опущенная на сторону a, b, c

Обратите внимание, что приведенные обозначения соответствуют рисунку, который находится выше, чтобы при решении реальной задачи по геометрии Вам визуально было легче подставить в нужные места формулы правильные значения.

Площадь треугольника равна половине произведения высоты треугольника на длину стороны на которую эта высота опущена (Формула 1). Правильность этой формулы можно понять логически. Высота, опущенная на основание, разобьет произвольный треугольник на  два прямоугольных. Если достроить каждый из них до прямоугольника с размерами b и h, то, очевидно, площадь данных треугольников будет равна ровно половине площади прямоугольника (Sпр = bh)
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними (Формула 2 ) (см. пример решения задачи с использованием этой формулы ниже). Несмотря на то, что она кажется непохожей на предыдущую, она легко может быть в нее преобразована. Если из угла B опустить высоту на сторону b, окажется, что произведение стороны a на синус угла γ по свойствам синуса в прямоугольном треугольнике равно проведенной нами высоте треугольника, что и даст нам предыдущую формулу
Площадь произвольного треугольника может быть найдена через произведение половины радиуса вписанной в него окружности на сумму длин всех его сторон (Формула 3), проще говоря, нужно полупериметр треугольника умножить на радиус вписанной окружности (так легче запомнить)
Площадь произвольного треугольника можно найти, разделив произведение всех его сторон на 4 радиуса описанной вокруг него окружности (Формула 4)
Формула 5 представляет собой нахождение площади треугольника через длины его сторон и его полупериметр (половину суммы всех его сторон)

Формула Герона (6) — это представление той же самой формулы без использования понятия полупериметра, только через длины сторон
Площадь произвольного треугольника равна произведению квадрата стороны треугольника на синусы прилежащих к этой стороне углов деленного на двойной синус противолежащего этой стороне угла (Формула 7)
Площадь произвольного треугольника можно найти как произведение двух квадратов описанной вокруг него окружности на синусы каждого из его углов. (Формула 8)
Если известна длина одной стороны и величины двух прилежащих к ней углов, то площадь треугольника может быть найдена как квадрат этой стороны, деленный на двойную сумму котангенсов этих углов (Формула 9)
Если известна только длина каждой из высот треугольника (Формула 10), то площадь такого треугольника обратно пропорциональна длинам этих высот, как по Формуле Герона
Формула 11 позволяет вычислить площадь треугольника по координатам его вершин, которые заданы в виде значений (x;y) для каждой из вершин

Обратите внимание, что получившееся значение необходимо взять по модулю, так как координаты отдельных (или даже всех) вершин могут находиться в области отрицательных значений

См. также площадь равнобедренного треугольника.

Примечание. Далее приведены примеры решения задач по геометрии на нахождение площади треугольника. Если Вам необходимо решить задачу по геометрии, похожей на которую здесь нет — пишите об этом в форуме. В решениях вместо символа «квадратный корень» может применяться функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Иногда для простых подкоренных выражений может использоваться символ √

Вычисления с помощью окружностей

На практике используются способы расчета площади треугольника с помощью вписанной или описанной окружности. В первом случае необходимо знать величины всех сторон и радиус вписанного элемента. Далее:

• найдите полупериметр (p);
• умножьте полученную величину на значение радиуса (r) окружности и получите площадь.

Совет. При неизвестном радиусе его рассчитывают по формуле: r = P/2π. P — длина окружности, π — математическая константа.

По описанной вокруг треугольника окружности также можно вычислить его площадь. Потребуется знать радиус:

• получите произведение всех сторон треугольника;
• умножьте радиус на 4;
• разделите первое значение на второе.

Важно! Формула:

Пример для треугольника со сторонами 3,4 и 5 см. Если описать окружность, касающуюся каждой его вершины, то ее радиус будет равняться 2,5. После подстановки величин в уравнение получите итоговое значение 6 см2.

Предложенный набор методов — базовый, но вовсе не исчерпывающий. Существуют более сложные способы решения задания с меньшим количеством вводных данных и многоступенчатым расчетом.

Площадь равностороннего треугольника

Теорема 3

Площадь равностороннего треугольника определяется как произведение квадрата стороны с числом $\frac{\sqrt{3}}{4}$.

Математически это выглядит следующим образом

$S=\frac{α^2\sqrt{3}}{4}$

где $α$ – сторона треугольника.

Доказательство.

Пусть нам дан равносторонний треугольник, у которого сторона равняется $α$. Проведем высоту $h$ (рис. 5).

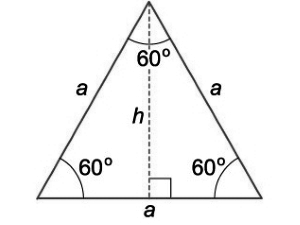
Высота равностороннего треугольника является также и медианой, значит, по теореме Пифагора

$h^2=α^2-\frac{α^2}{4}$

$h^2=\frac{3}{4} α^2$

$h=\frac{α\sqrt{3}}{2}$

Значит по теореме 1:

$S=\frac{α^2\sqrt{3}}{4}$

Теорема доказана.

Пример 3

Найти площадь равностороннего треугольника, если его сторона равняется $2$.

Решение.

Используя теорему 3, получим

$S=\frac{4\sqrt{3}}{4}=\sqrt{3}$

Ответ: $\sqrt{3}$.

Для равнобедренного треугольника

Рассмотрим случаи нахождения площади, если у треугольника равные боковые стороны.

Через основание и сторону

 В этом случае формула будет выглядеть следующим образом:

\(S=\frac b4\sqrt{4a^2-b^2}\)

где a — одно из боковых ребер фигуры, а b — ее основание.

Через основание и противолежащий угол

Зная длину основания и противолежащий ему угол, мы можем использовать следующую формулу:

\(S=\frac{b^2}{4\tan\left({\displaystyle\frac\beta2}\right)}\)

где b — основание многоугольника, β — противолежащий ему угол.

Через основание и высоту

Если нам известна величина основания равнобедренного треугольника, а также его высота, найдем S по приведенной ниже по элементарной формуле:

\(S=\frac{b\times h}2\)

где b — основание фигуры, а h — высота, проведенная к этому основанию.

Через боковые стороны и угол между ними

Если мы знаем длину боковых сторон и угол между ними, найдем площадь, опираясь на расчеты:

\(S=\frac12a^2\times\sin\left(\beta\right)\)

где a — это боковое ребро, β — угол между равными ребрами.

Через основание и угол между боковыми сторонами

В этом случае нам сначала придется найти высоту по формуле:

\(h=\frac b2\tan\left(\beta\right)\)

где β — угол при вершине, а b — основание.

Далее подставляем значение в формулу

\(S=\frac{b\times h}2 = \frac{b\times{\displaystyle\frac b2}\tan\left(\beta\right)}2=\frac{b^2\tan\left(\beta\right)}4\)

Итоговая формула:

\(S=frac{b^2\tan\left(\beta\right)}4\)

Как рассчитать площадь?

От качества выполнения работы по кровельному настилу зависит последующая комфортность проживания в жилом помещении. Чтобы правильно высчитать площадь крыши, нужно учесть тип и форму кровельного материала, а также особенности конструкции жилища. Точные вычисления позволяют сделать строение крыши надежным и прочным, определить количество денежных вложений.

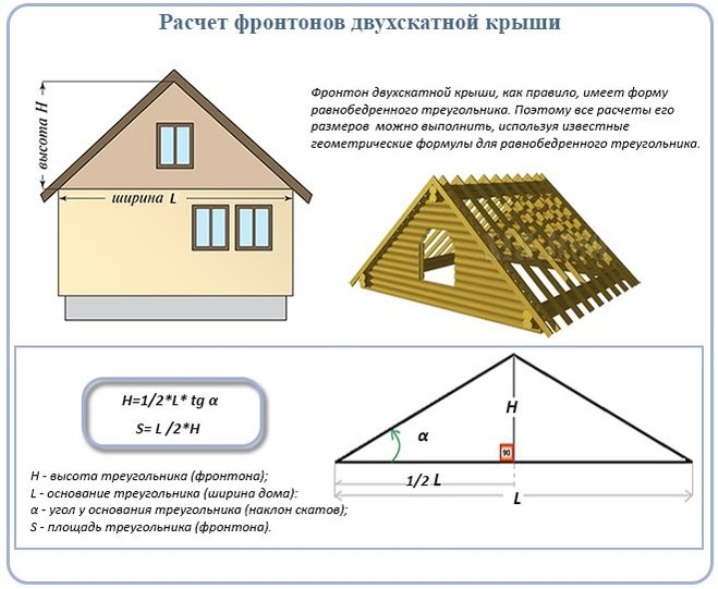
Для этого могут быть использованы различные материалы, например, шифер, профнастил или металлочерепица, а также доборные комплектующие элементы. Листы кровли принято укладывать внахлест. Поэтому на каждую сторону крыши потребуется порядка 10-15% для продольного нахлеста.

Вычислить площадь кровли можно посредством выполнения необходимых замеров. При этом следует учитывать следующие факторы:

• площадь по углу наклона и геометрическому строению крыши;
• наличие на крыше люков и иных элементов, которые не будут покрыты кровельным настилом;
• выбранная теплоизоляция, тип утеплителя и облицовки.

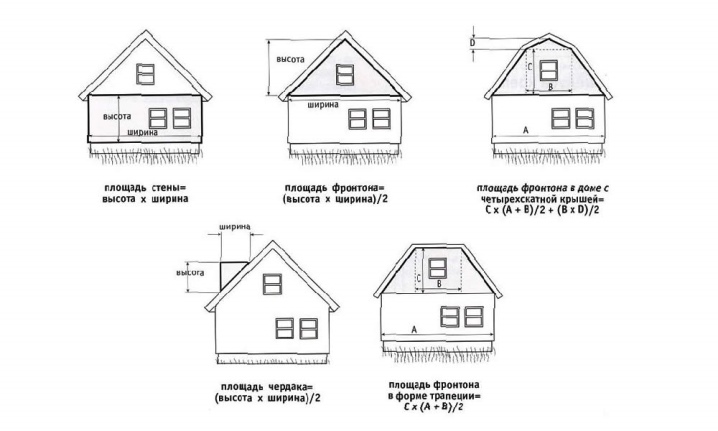
Определение площади крыши предполагает вычисление высоты, угла наклона и объема стройматериалов. Грамотно рассчитав квадратуру, можно сэкономить на покупке кровли и транспортировке материалов. Однако следует закупать кровельные материалы с небольшим запасом во избежание их недостатка при монтаже или при допущении ошибок в укладке. При сложной конфигурации крыши с несколькими скатами придется рассчитать параметры геометрических фигур.

Площадь высчитывается по формуле в зависимости от формы ската:

• трапециевидный: (A+B) *H/2;
• прямоугольный: A*B;
• параллелограмм: A*H;
• равносторонний треугольник: (A*H) /2.

Где A – ширина кровли, B – длина кровли, H – высота треугольника.

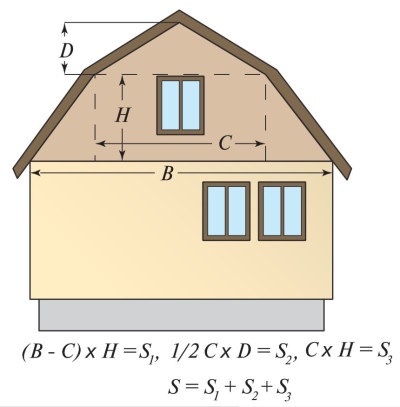
Для простоты расчетов рекомендовано разделить сложные геометрические фигуры на простые элементы, а затем найти суммарную площадь полученных значений в квадратных метрах.

Для измерения площади треугольника фронтона нужно провести замеры длины торцевой стены и поделить ее пополам. Полученную величину умножить на tg угла, образуемого между скатом и основанием крыши.

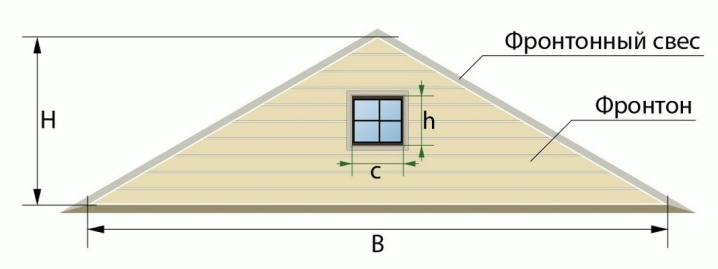
Треугольный скат является наиболее распространенной геометрической конфигурацией домовладений. Ломаная разновидность крыши имеет более сложную конструкцию. Ее возведение затрудняется устройством стропильной системы и требуемыми расчетами.

1 Общие формулы для вычисления площади треугольника

Формула площади треугольника по длине и высоте

S= a*h/2,
где а – это длина стороны треугольника, площадь которого нужно найти, h-длина проведенной к основанию высоты.

Формула Герона

S=√р*(р-а)*(р-b)*(p-c),
где √-это квадратный корень, p-полупериметр треугольника, a,b,c-это длина каждой стороны треугольника. Полупериметр треугольника можно вычислить по формуле p=(a+b+c)/2.

S = (a*b*sin(α))/2,
где b,c -это длина сторон треугольника, sin(α)- синус угла между двумя сторонами.

Формула площади треугольника по радиусу вписанной окружности и трем сторонам

S=p*r,
где p-это полупериметр треугольника, площадь которого нужно найти, r-радиус вписанной в этот треугольник окружности.

Формула площади треугольника по трем сторонам и радиусу описанной вокруг него окружности

S= (a*b*c)/4*R,
где a,b,c-это величина длины каждой стороны треугольника, R- радиус описанной вокруг треугольника окружности.

Формула площади треугольника по декартовым координатам точек

Декартовы координаты точек – это координаты в системе xOy, где x- это абсцисса, y- ордината. Декартовой системой координат xOy на плоскости называют взаимно перпендикулярные числовых оси Oх и Oy с общим началом отсчета в точке О. Если заданы координаты точек на этой плоскости в виде A(x1, y1), B(x2, y2) и C(x3, y3), то можно вычислить площадь треугольника по следующей формуле, которая получена из векторного произведения двух векторов.
S = |(x1 – x3)•(y2 – y3) – (x2 – x3)•(y1 – y3)|/2,
где || обозначает модуль.

Вывод формул для площади произвольного треугольника

      Утверждение 1. Площадь треугольника можно найти по формуле

где a – любая сторона треугольника, а h_a – , опущенная на эту сторону.

      Доказательство.

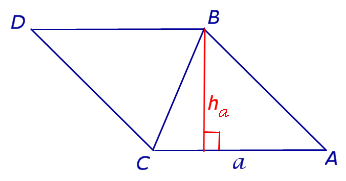
Рис. 1

Достроив треугольник ABC до ABDC (рис. 1),

что и требовалось доказать.

      Утверждение 2. Площадь треугольника можно найти по формуле

где a и b – две любые стороны треугольника, а С – угол между ними.

      Доказательство.

Рис. 2

Поскольку

h_a = b sin C ,

то, в силу утверждения 1, справедлива формула

что и требовалось доказать.

      Утверждение 3. Площадь треугольника можно найти по формуле

где a – любая сторона треугольника, а B, С – прилежащие к ней углы.

      Замечание. Докажем утверждение 3 в случае . Доказательство в случаях требует лишь незначительных изменений, совершить которые мы предоставляем читателю в качестве самостоятельного упражнения.

      Доказательство.

Рис. 3

Поскольку (рис.3)

x = h_actg C ,       y = h_actg B ,

то

a = x + y == h_actg C + h_actg B == h_a( ctg C + ctg B) .

      Следовательно,

      Поэтому

что и требовалось доказать.

      Утверждение 4. Площадь треугольника можно найти по формуле

где a, b, c – стороны треугольника, а r – радиус .

      Доказательство.

Рис. 4

Соединив центр O вписанной окружности с вершинами треугольника (рис.4), получим

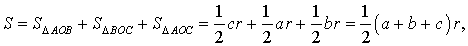
что и требовалось доказать.

      Утверждение 5. Площадь треугольника можно найти по формуле

где a, b, c – стороны треугольника, а R – радиус .

      Доказательство.

Рис. 5

В силу справедливо равенство

.

      Следовательно,

      Поэтому

что и требовалось доказать.

      Утверждение 6. Площадь треугольника можно найти по формуле:

S = 2R2 sin A sin B sin C ,

где A, B, С – углы треугольника, а R – радиус .

      Доказательство.

Рис. 6

В силу справедливо равенство

.

      Поэтому

a = 2R sin A ,     b = 2R sin B ,     c = 2R  sin C ,

      В силу утверждения 5

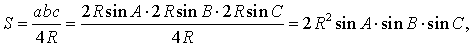
что и требовалось доказать.